| Definitions | Type, False, MaInterface(T), (x  l), x:A l), x:A  B(x), B(x),  x:A. B(x), s = t, {T}, x:A x:A. B(x), s = t, {T}, x:A  B(x), P B(x), P   Q, Q,  x:A. B(x), SQType(T), x:A. B(x), SQType(T),  , strong-subtype(A;B), s ~ t, left + right, , strong-subtype(A;B), s ~ t, left + right,  , #$n, , #$n,  , ff, Void, True, Unit, ma-interface-loc(I;i), {x:A| B(x)} , Knd, State(ds), hasloc(k;i), , ff, Void, True, Unit, ma-interface-loc(I;i), {x:A| B(x)} , Knd, State(ds), hasloc(k;i),  x.A(x), x.A(x),   x. t(x), Atom$n, a < b, ma-interface-locs(I), ma-interface-dom(I;i), case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , type List, S x. t(x), Atom$n, a < b, ma-interface-locs(I), ma-interface-dom(I;i), case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , type List, S  T, Outcome, A T, Outcome, A  B, ||as||, B, ||as||,  A, A,  , l[i], |g|, A c , l[i], |g|, A c B, P & Q, P B, P & Q, P   Q, [car / cdr], P Q, [car / cdr], P  Q, P Q, P    Q, hd(l), last(L), Q, hd(l), last(L),  , IdDeq, x , IdDeq, x  dom(f), dom(f),  b, Top, Id, a:A fp b, Top, Id, a:A fp B(a), t B(a), t  T, null(as), T, null(as),   b, tt, b, tt, 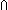 x:A.B(x), <a, b>, i <z j, i x:A.B(x), <a, b>, i <z j, i  z j, n+m, i z j, n+m, i  j < k, i j < k, i 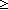 j , {i..j j , {i..j }, }, 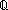 , IdLnk, p =b q, (i = , IdLnk, p =b q, (i =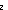 j), x =a y, a < j), x =a y, a < b, f(a), x f y, a < b, f(a), x f y, a < b, [d] b, [d] , eq_atom$n(x;y), q_le(r;s), q_less(a;b), qeq(r;s), a = b, a = b, deq-member(eq;x;L), p , eq_atom$n(x;y), q_le(r;s), q_less(a;b), qeq(r;s), a = b, a = b, deq-member(eq;x;L), p    q, p q, p   q, p q, p   q, [], tl(l), n - m, if a<b then c else d, nth_tl(n;as), rec-case(a) of [] => s | x::y => z.t(x;y;z), Y, Dec(P), b | a, a ~ b, a q, [], tl(l), n - m, if a<b then c else d, nth_tl(n;as), rec-case(a) of [] => s | x::y => z.t(x;y;z), Y, Dec(P), b | a, a ~ b, a  b, a <p b, a < b, b, a <p b, a < b,  x x L. P(x), ( L. P(x), ( x x L.P(x)), r L.P(x)), r  s, r < s, q-rel(r;x), l_disjoint(T;l1;l2), (e <loc e'), e s, r < s, q-rel(r;x), l_disjoint(T;l1;l2), (e <loc e'), e  loc e' , (e < e'), e c loc e' , (e < e'), e c e', e',  e<e'.P(e), e<e'.P(e),  e e e'.P(e), e'.P(e),  e<e'. P(e), e<e'. P(e),  e e e'.P(e), e'.P(e),  e e [e1,e2).P(e), [e1,e2).P(e),  e e [e1,e2).P(e), [e1,e2).P(e),  e e [e1,e2].P(e), [e1,e2].P(e),  e e [e1,e2].P(e), [e1,e2].P(e),  e e (e1,e2].P(e), es-r-immediate-pred(es;R;e';e), same-thread(es;p;e;e'), [e: i (e1,e2].P(e), es-r-immediate-pred(es;R;e';e), same-thread(es;p;e;e'), [e: i   p p  j], [e: i j], [e: i   p p  j], f2f+-pred(e',e), fpf-domain(f), EqDecider(T) j], f2f+-pred(e',e), fpf-domain(f), EqDecider(T) |